Chinese Remainder Theorem

When dividing numbers $0,1,2,3,\dots$ by (say) $5$, we get remainders

$0,1,2,3,4,0,1,2,3,4,0,1,2,\dots :$ this repeats all the time. In general, $m$ and $m+5$ have the same remainder ($m\equiv m+5(mod5)$, their difference is divisible by $5$).

What if we consider the remainders for two different modulo at the same time?

First of all, we choose a pair like $2$ and $3$ for dividing a number for example $15$.

• The remainders modulo $2$ (i.e., $0$ and $1$) alternate (even values of $i$ alternate with odd values of $i$).

• The remainders modulo $3$ (i.e., $0,1,2$) appear in a $3$-loop ($0,1,2,0,1,2,\dots$)

• When we come to six, both cycles return to their original position (since $6$ is divisible both by $2$ and $3$, and then the pairs start to repeat, thus forming a loop of length $6$).

• All six possible combinations of remainders (two possible remainders modulo $2$ combined with three possible remainders modulo $3$) appear in this sequence (once per a $6$-loop).

Let us look at the column for $2$ and $4$: we see a cycle of length $4$ in this column formed by pairs $(0,0),(1,1),(0,2),(1,3)$ - and, indeed, $4$ is divisible both by $2$ and $4$, so we get again the pair $(0,0)$. Note that not all combinations of remainders appear in the cycle: for example, pair $(1,2)$ does not appear.

Can you explain why this pair does not appear: why there are no m such that $m\equiv 0(mod4)$ and $m\equiv 1(mod6)$?

Again, the reason is simple: numbers of the form $4u+0$ are even, while numbers of the form $6v+1$ are odd.

To understand the behavior of remainders, it is useful to look at bigger examples, and draw the pairs of remainders on a coordinate plane. This can be done with the following code (do not worry if you do not understand the options, they are needed to make nice plots).

import matplotlib.pyplot as plt

a, b = 10, 5
n = a * b

plt.plot([i % a for i in range(n)], [i % b for i in range(n)],
         color='green', linestyle='dashed', linewidth=3,
         marker='o', markerfacecolor='blue', markersize=12)

plt.axis('square')
plt.xlim(-1, a)
plt.ylim(-1, b)
plt.xlabel(f'm mod {a}')
plt.ylabel(f'm mod {b}')

plt.savefig('crt-10-5.png')

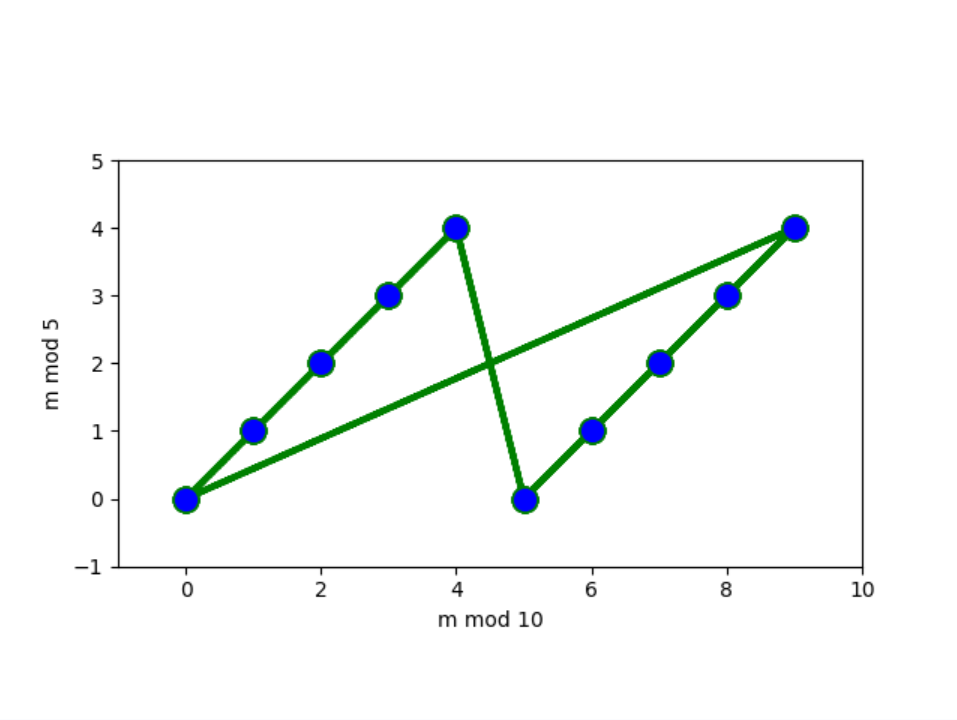
In the first picture, the remainder modulo $10$ determines the remainder modulo $5$. Indeed, if $m=10k+r$, then $10k$ is divisible by $5$, so $mmod5=rmod5$.

A similar picture for $mmod13$ and $mmod7$ looks different:

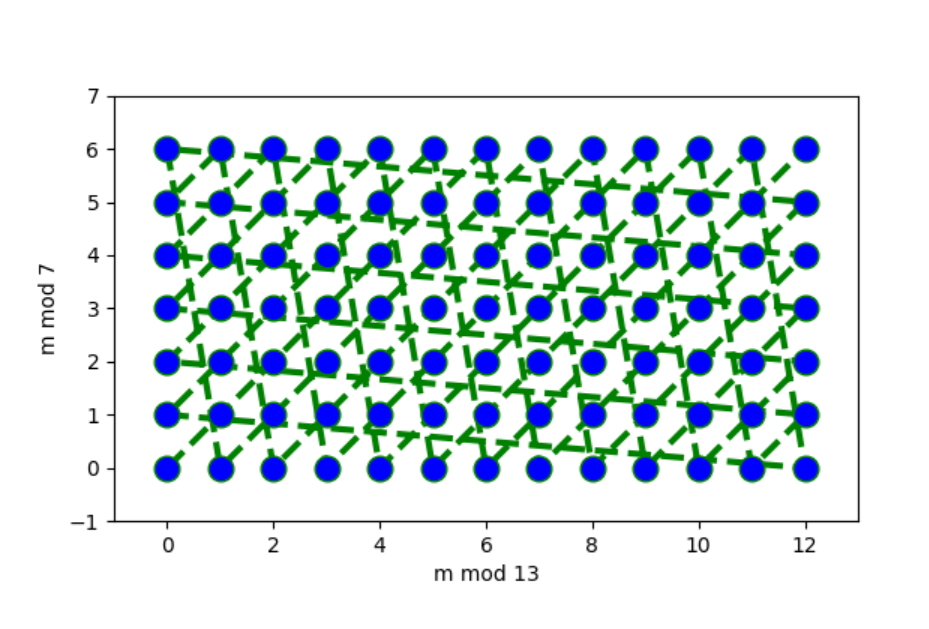
Here we see that all pairs of remainders are possible. Why? This question is answered by the Chinese remainder theorem.

Theorem

Let $p,q$ be coprime. Then the system of equations $$x=a(modp)$$ $$x=b(modq)$$

has a unique solution for $x$ modulo $pq$.

The reverse direction is trivial: given $x\in {\mathbb{Z}}_{{}_{pq}}$ we can reduce $x$ modulo $p$ and $x$ modulo $q$ to obtain two equations of the above form.

The following is a general construction to find a solution to a system of congruences using the Chinese remainder theorem:

1. Compute $N=n_1\times n_2\times \cdots \times n_k$

2. For each $i=1,2,\dots ,k$ compute $$y{}_i=\frac{N}{n{}_i}=n_1\cdot n_2+\cdots +n_{{}_{i-1}}\cdot n_{{}_{i+1}}+\cdots +n{}_k$$

3. For each $i=1,2,\dots ,k$ compute $z_i\equiv y_i^{-1}mod{n}_i$ using Euclid's extended algorithm ($z_i$ exists since $n_1,n_2,\dots ,n_k$ are pairwise coprime).

4. The integer $x={{\sum }^k}_{{}_{i=1}}{a}_i{y}_i{z}_i$ is a solution to the system of congruences, and $xmodN$ is the unique solution modulo $N$.

When a system contains a relatively small number of congruences, an efficient process exists to apply the Chinese remainder theorem.

Solve the system of congruences

$$x\equiv 1mod3$$ $$x\equiv 4mod5$$ $$x\equiv 6mod7$$ Take all the yi and construct the integer: $$M=a_1{M}_1{y}_1+a_2{M}_2{y}_2+...+a_r{M}_r{y}_r$$ We can prepare our situation to this: $$a_1=1a_2=4a_3=6$$ $$M_1=5\cdot 7M_2=3\cdot 7M_3=3\cdot 5$$ We wrote $x_n^{-1}$ instead $y_n$ for inverse $$x=5\cdot 7\cdot 1\cdot x_1^{-1}+3\cdot 7\cdot 4\cdot x_2^{-1}+3\cdot 5\cdot 6\cdot x_3^{-1}$$ $$\text{for mod 3}\text{ for mod 5}\text{ for mod 7}$$ For find to general $x$ solve inverses of $x$ values $$M_n\cdot x_n^{-1}=1\mathrm{mod}(m)$$ For $x_1^{-1}$: $$5\cdot 7\cdot x_1^{-1}\equiv 1\mathrm{mod}(3)$$ $$3\cdot x_1^{-1}\equiv 1\mathrm{mod}(3)$$ We can use extended euclid algortihm $$3=2\cdot 1+1$$ $$1=3-2\cdot 1$$ $$x_1^{-1}=-1=2$$ find all $x$ values like this: $$x_2^{-1}=1,x_3^{-1}=1$$ and combine together: $$x=(5\cdot 7\cdot 1\cdot 2+3\cdot 7\cdot 4\cdot 1+3\cdot 5\cdot 6\cdot 1)\mathrm{mod}(3\cdot 5\cdot 7)$$ $$x=(70+84+90)\mathrm{mod}(105)$$ $$x=(244)\mathrm{mod}(105)$$ $$x=(34)\mathrm{mod}(105)$$

Question-1 :  A box contains gold coins.

If the coins are equally divided among six friends, four coins are left over.

If the coins are equally divided among five friends, three coins are left over.

If the box holds the smallest number of coins that meets these two conditions, how many coins are left when equally divided among seven friends?

See answer ▼

Answer : 0

First of all, mathematize the question. $$x\equiv 4\mathrm{mod}(6),x\equiv 3\mathrm{mod}(5)$$ So, $$x\equiv y\mathrm{mod}(7)?$$ We can prepare our situation $$a_1=4,a_2=3$$ $$M_1=5,M_2=6$$ $$x=5\cdot 4\cdot x_1^{-1}+6\cdot 3\cdot x_2^{-1}$$ $$\text{for mod 6}\text{for mod 5}$$ For $x_1^{-1}$ and $x_2^{-1}$ : $$5\cdot x_1^{-1}\equiv 1\mathrm{mod}(6)$$ $$6\cdot x_2^{-1}\equiv 1\mathrm{mod}(5)$$ $$x_1^{-1}=5,x_2^{-1}=1$$ general equation: $$x=(5\cdot 5\cdot 4+6\cdot 3\cdot 1)\mathrm{mod}(6\cdot 5)$$ $$x=118\mathrm{mod}(30)$$ $$x=28\mathrm{mod}(30)$$ we found $28$ gold in our box. Now divide among seven friends $$28\equiv y\mathrm{mod}(7)$$ $$0\equiv y\mathrm{mod}(7)$$ Opps, zero coins left after divided our friends :)

Example

Find $x$, if possible, such that $$2x\equiv 5\mathrm{mod}(7)$$ $$3x\equiv 4\mathrm{mod}(8)$$

Solution First note that $2$ has an inverse modulo $7$, namely $4$. So we can write the first equivalence as $x\equiv 4\cdot 5\equiv 6\mathrm{mod}(7)$. Hence, we can multiply every side of equation with inverse of $2$. $$2\cdot 4\cdot x\equiv 5\cdot 4\mathrm{mod}(7)$$ $$8\cdot x\equiv 20\mathrm{mod}(7)$$ and we reached simple equation $$x\equiv 6\mathrm{mod}(7)$$ do it same process for other $$3\cdot 3\cdot x\equiv 4\cdot 3\mathrm{mod}(8)$$ $$x\equiv 4\mathrm{mod}(8)$$ We can revise the question again and solve it like the previous ones. I left this to you :)