Welcome to your-notes.

∴

lorem ipsum dolor sit amet

— your-name

Welcome to Number Theory and Cryptography notes.

∴

I completed the course by taking detailed notes and summarizing critical concepts for future reference.

University of California San Diego

Instructor: Michael Levin

— emreaslan —

Numbers

Most of the concepts we learn in math seem pretty far removed from our everyday lives. We might think, "Who really needs to know about calculus or trigonometry?" But the truth is, even the most basic mathematical ideas have their roots in real-world problems. Let's go back to the very beginning and see how it all started...

Once upon a time, in a big, dark cave, there lived a caveman named Grog. Grog had a bunch of sheep. He wanted to know how many sheep he had, so he started counting, $1,2,\mathrm{3...}$ And just like that, he discovered counting numbers or natural numbers ($N$). Pretty cool, huh?

But then, a sneaky caveman named Ug came along and stole some of Grog’s sheep! Ug told Grog that he needed to give him 3 more sheep. Grog was upset, but he started thinking. If he wanted to have 3 sheep left, he needed to have 6 sheep in total to give 3 to Ug. This is how Grog discovered negative numbers ($...-3,-2,-1$) and integers ($...-3,-2,-1,0,1,2,\mathrm{3...}$)

Later, Grog had 3 delicious berries. He wanted to share them with his family of 4. But wait, he couldn’t divide 3 berries into 4 equal parts! That’s when Grog discovered rational numbers $R$(fractions). Even though he couldn’t share them equally, he learned that sometimes, numbers can be broken into smaller pieces.

Number theory is all about studying whole numbers and how they work together. It started out with practical uses, but as it got more complex, it seemed less useful in real life.

After interesting researches about cryptography and electric fiels, number theory, even the really complicated parts, is super important for modern cryptography. And cryptography is a big deal in our lives. It's what keeps our emails, messages, online shopping, and the whole internet safe.

Divisibility

When we say that a number $a$ is divisible by $a$ number $b$, we mean that $a$ can be divided by $b$ without leaving a remainder. In other words, $a$ is $a$ multiple of $b$.

Example:

$15$ is divisible by $3$ because $15$ divided by $3$ equals $5$ without any remainder. $15$ is not divisible by $4$ because 15 divided by $4$ leaves a remainder of $3$.

Formal Definition:

We can write this mathematically as:

If $a$ is divisible by $b$, we can write $a$ as $b$ multiplied by another integer $k$. In symbols: $a=b\cdot k$.

Equivalently, we can use the vertical line notation: $b\mid a$. This means b divides a.

Example:

$15$ is divisible by $3$ because $15=3\cdot 5$. Therefore, we can also write $3\mid 15$.

Checking Divisibility in Python:

In Python, we can use the modulo operator (%) to check if a number is divisible by another. If the remainder is $0$, then the first number is divisible by the second.

print(15 % 3 == 0) # Output: True
print(15 % 4 == 0) # Output: False

Properties of Divisibility:

• $lemma$: If $c$ divides $a$ and $b$, then $c$ divides $a\pm b$.

  $proof$: Since $c$ divides $a$, there is $k_1$ such that $a=c\cdot k_1$. Similarly, there is $k_2$ such that $b=c\cdot k_2$. Then

  $$a\pm b=c\cdot k_1\pm c\cdot k_2=c\cdot (k_1\pm k_2)$$

• $lemma$: If $b\mid a$, then for any integer $c$, $b\mid (a\cdot c)$.

  $proof$: Since $b\mid a$, we have that $a=b\cdot k$ for some $k$. We can multiply both sides of equality by $c$: $c\cdot a=b\cdot (c\cdot k)$. By defination, this means that $c\cdot a$ is divisible by $b$.

Quiz - Division by 101

These properties are essential for understanding divisibility and proving various mathematical theorems.

As you can see, divisibility is a fundamental concept in mathematics that has practical applications in various fields, from computer science to cryptography.

Remainders

In our previous exploration of integer division, we encountered situations where one integer couldn't be perfectly divided by another. This led us to the concept of divisibility. Now, let's delve deeper into the mechanics of integer division when it's not exact.

Defination

Given two integers, $a$ and $b$ (where $b$ is positive), the division with remainder of $a$ by $b$ is a pair of integers, $q$ (quotient) and $r$ (remainder), satisfying the following conditions:

$$a=q\cdot b+r$$ $$0\le r<b$$

Think of $a$ as a collection of objects. We want to divide these objects into groups of size $b$. The quotient, $q$, represents the number of complete groups we can form, while the remainder, $r$, is the number of objects left over after forming the groups.

• $15/4=3\cdot 4+3$ , So, $q=3$ and $r=3$

• $-13/3=-5\cdot 3+2$ , So, $q=-5$ and $r=2$

• $12/4=3\cdot 4+0$ , So, $q=3$ and $r=0$ (in this case, a is divisible by b, $b\mid a$).

def divide_with_remainder(a, b):
  "Divides a by b and returns the quotient and remainder."
  q = a // b
  r = a % b
  return q, r

# Examples
a, b = 15, 4
q, r = divide_with_remainder(a, b)
print(f"{a} = {q} * {b} + {r}")

Algorithms

If we consider numbers that have the same remainder when divided by $a$ specific number, we can observe interesting patterns. For example, numbers that leave a remainder of $1$ when divided by $7$ have the form: $$a=7\cdot q+1$$

where $q$ is any integer. This pattern can be extended to any divisor and any remainder. For example, this pattern creates own group by given $q$. For positive $q=1,2,\mathrm{3..}$ we get sequence $a=8,15,\mathrm{22..}$ For negative $q=-1,-2,-\mathrm{3...}$ we get sequence $a=-6,-13,-\mathrm{20...}$

Overall, this is our group would be like this:

Exercise

Conclusion

Division with remainder is a fundamental concept in number theory that allows us to understand the relationships between integers and their divisibility properties.

It has applications in various areas of mathematics and computer science.

Modular Arithmetic

What is the remainder when this expression is divided by 3? $$17\cdot (12\cdot 19+5)-23$$

It seems like it will take some time to calculate the result of the operation. Maybe, we choose another way to solve this. But first, we must examine modular artihmetic deeply.

Definition :  We say that two numbers $a$ and $b$ are congruent modulo $m$ if they have the same remainder when divided by $m$. This donete by $$a\equiv b\mathrm{mod}m$$

In other words, a number $a$ is congruent modulo $m$ to all numbers $a+k\cdot m$ for integer $k$. In particular, if $r$ is remainder of $a$ when divided by $m$ then $a\equiv r\mathrm{mod}m$.

Key Lemmas and Properties

Addition

• If $a\equiv b\mathrm{mod}m$, then $a+c\equiv b+c\mathrm{mod}m$ for any $c$.
• If $a\equiv b\mathrm{mod}m$ and $c\equiv d\mathrm{mod}m$, then $a+c\equiv b+d\mathrm{mod}m$.

Multiplication

• If $a\equiv b\mathrm{mod}m$, then $a\cdot c\equiv b\cdot c\mathrm{mod}m$ for any $c$.
• If $a\equiv b\mathrm{mod}m$ and $c\equiv d\mathrm{mod}m$, then $a\cdot c\equiv b\cdot d\mathrm{mod}m$.

These lemmas essentially state that we can perform addition and multiplication on congruent numbers without changing their congruence modulo $m$.

Example

To find the remainder of $14+41+20+13+29$ when divided by $4$, we can replace each number with its equivalent modulo $4$:

$$14\equiv 2\mathrm{mod}4,41\equiv 1\mathrm{mod}4,20\equiv 0\mathrm{mod}4,13\equiv 1\mathrm{mod}4,29\equiv 1\mathrm{mod}4$$

Then, the sum becomes:

$$2+1+0+1+1\equiv 5\equiv 1\mathrm{mod}4$$

Therefore, the remainder is 1.

Now we are ready to solve the problem that asked us to calculate the remainder of when divided by $3$. $$17\cdot (12\cdot 19+5)-23$$

To compute the remainder, we can substitute each number by their remainder when divided by 3. As we have seen, this change does not affect the remainders of the results of arithmetic operations. This gives us

$$17\cdot (12\cdot 19+5)-23=2\cdot (0\cdot 1+2)+1\equiv 2\mathrm{mod}3$$

This simplifies computation a lot. This way, the computer does not consume much computing power.

Modular Subtraction and Division

Modular Subtraction

Modular subtraction is a straightforward operation within the realm of modular arithmetic. It follows intuitively from the properties of modular addition.

Definition:   Given two integers $a$ and $b$, and $a$ modulus $m$, the modular subtraction of $a$ from $b$ modulo $m$ is defined as finding an integer $x$ such that:

$$b-a\equiv x\mathrm{mod}m$$

This is equivalent to finding a number $x$ that, when added to $a$, gives $b$ modulo $m$.

Example:

Find $x$ such that $13-7\equiv x\mathrm{mod}5$. We can calculate directly: $13-7=6$. Since $6\equiv 1\mathrm{mod}5$, we have $x=1$.

Modular subtraction is closed under the set of integers modulo m. That is, the result of modular subtraction is always an integer between 0 and m-1.

Modular Division

Modular division is more complex than modular subtraction and is not always defined.

Definition:   Given two integers $a$ and $b$, and $a$ modulus $m$, the modular division of $b$ by $a$ modulo $m$ is defined as finding an integer $x$ such that:

$$a\cdot x\equiv b\mathrm{mod}m$$

This $x$ is often called the modular multiplicative inverse of $a$ modulo $m$.

Not Always Defined

Unlike modular addition and subtraction, modular division is not always defined. For example, consider the equation $$2\cdot x\equiv 1\mathrm{mod}4$$ There is no integer $x$ that satisfies this equation.

Is there a way when the division is possible and when it is not? We will figure this out soon!

The things turn out to be rather complicated. On the one hand, it is bad: it is nice when the computations and calculations are simple. On the other hand, this is good: complicated things are crucial for cryptography.

Questions

Question-3 :   What are the last two digits of the number $99^{99}$?

The number $99^{99}$ is huge, we do not want to compute it. Instead, we can use remainders. Note that the number consisting of the last two digits is just the remainder after the division by $100$. Thus, we are actually interested in the remainder of the number $99^{99}$ when divided by $100$.

Note that $99\equiv -1\mathrm{mod}100$. This allows us to simplify the computation a lot: $$99^{99}\equiv (-1{)}^{99}\equiv -1\equiv 99\mathrm{mod}100$$

Thus, the remainder of $99^{99}$ when divided by $100$ is $99$ and these are the two last digits of $99^{99}$.

In the computation above we used that $99^{99}$ is just $99$ multiplied by itself $99$ times. We then use that in the multiplication modulo some number we can substitute the numbers by their congruent.

Note that one cannot just substitute any number in any expression by its congruent. For example, we cannot substitute $99^{99}$ by $(-1{)}^{-1}$ We have only proved that we can substitute numbers by their congruents in additions and multiplications, and we should be careful to use only these properties.

Question-4 :   Is the number $3475$ divisible by $3$?

To solve this problem it is enough to compute the remainder of the number after the division by $3$: the number is divisible by $3$ if the remainder is $0$.

But how can we compute the remainder fast? We can try the same approach we used for divisibility tests. Observe that $$3475=3000+400+70+5=3\cdot 10^3+4\cdot 10^2+7\cdot 10+5$$

Now we represented our number as an arithmetic expression and we can use modular arithmetic. Note that $$10\equiv 1\mathrm{mod}3$$

Thus, for any positive $k$ $$10^k\equiv 1^k\equiv 1\mathrm{mod}3$$

Applying this to our number, we get $$3475\equiv 3\cdot 10^3+4\cdot 10^2+7\cdot 10+5\equiv 3+4+7+5\mathrm{mod}3$$

Now $$3+4+7+5\equiv 19\equiv 1\mathrm{mod}3$$

Thus, the remainder of $3475$ when divided by $3$ is $1$ and $3475$ is not divisible by $3$.

Note, that the same argument can be applied in a general setting, giving the following lemma.

Question-6 :   Find a remainder $x$ such that $3\cdot x\equiv 5\mathrm{mod}7$?

We must multiply $3$ by such an integer that when we divide the resulting number by $7$, $5$ gives the remainder.

The first positive number that gives a remainder of $5$ is $5$. However, we cannot get $5$ by multiplying a positive number by $3$. Let's try the number sequence starting from $5$ and increasing by $7$. $$5,12,19,26,33,\mathrm{40...}$$ the quotient of every number divisible by $3$ in this group is our answer. The smallest correct answer for $x$ is $4$.

Question-7 :   Find a remainder $x$ such that $12\cdot x\equiv 3\mathrm{mod}7$?

Again, try the way just before. But first of all, we can minimize this problem to $$5\cdot x\equiv 3\mathrm{mod}7$$

Now, We must multiply $5$ by such an integer that when we divide the resulting number by $7$, $3$ gives the remainder. We create possible group like this: $$3,10,17,24,31,38,45,\mathrm{52...}$$ However, we cannot get $3$ by multiplying a positive number by $5$. $10$ and $45$ are the numbers divisible by $5$ at the beginning of the group and these constitute our answers. The smallest $x$ value will be $2$.

Of course, we can create correct answer group like this: $$2,9,16,\mathrm{23...}$$

Greatest Common Divisor

  The greatest common divisor (GCD) of two integers, $A$ and $B$, is the largest positive integer that divides both A and B without leaving a remainder. It's a fundamental concept in number theory with applications in various fields, including cryptography and computer science.

Key Properties of the GCD

• Divisibility:   Any common divisor of $A$ and $B$ must also divide their GCD.
• Uniqueness:   For any given $A$ and $B$, there exists a unique GCD.
• Non-Trivial Case:   If $A$ and $B$ are not both zero, their GCD is always positive.

The Naive Approach: Inefficient Brute Force

  A straightforward method to compute the GCD is to iteratively check all possible divisors from the minimum of $A$ and $B$ down to $1$.

However, this approach becomes extremely inefficient for large numbers, as the number of iterations grows linearly with the minimum value.

You can try this python code on your computer. First try small numbers you see solution in miliseconds but if you try large numbers you can hear the sound of the computer's fans 😁

def gcd(a, b):
  assert a >= 0 and b >= 0 and a + b > 0

  if a == 0 or b == 0:
    return max(a, b)

  for d in range(min(a, b), 0, -1):
    if a % d == 0 and b % d == 0:
      return d

  return 1

print(gcd(0, 1))
print(gcd(24, 16))
# The following call would take too long
#print(gcd(790933790547, 1849639579327))

Motivation for an Efficient Algorithm

  The need for an efficient GCD algorithm arises from its applications in computationally intensive tasks. For example, in cryptography, the GCD is used in algorithms like the RSA encryption scheme. A slow GCD algorithm can significantly impact the performance of these cryptographic systems.

The Euclidean Algorithm: A More Efficient Approach

  The Euclidean algorithm is a classical method for efficiently computing the greatest common divisor (GCD) of two numbers. It is based on the principle that the GCD of two numbers also divides their difference. This algorithm is not only simple but also significantly faster than the naive approach of checking all possible divisors.

In the next lesson, we will delve into the Euclidean algorithm in detail. We will explore its mathematical foundation, step-by-step procedure, and various optimizations that can be applied to further enhance its performance. Additionally, we will implement the algorithm in code and discuss its applications in different computational tasks, including cryptography and number theory.

Euclid's Algorithm

Euclid's algorithm, a cornerstone of number theory, provides an efficient method for calculating the greatest common divisor (GCD) of two integers. This ancient algorithm, attributed to the Greek mathematician Euclid, has found widespread applications in various fields, from cryptography to computer science.

The algorithm's foundation lies in the following lemma:

Euclid's Lemma:  An integer $d$ divides both integers $a$ and $b$ if and only if $d$ divides $a-b$ and $b$.

This lemma can be intuitively understood by considering a visual representation. If $a$ and $b$ can be divided into equal-sized groups of $d$, then their difference, $a-b$, can also be divided into the same-sized groups.

Conversely, if $a-b$ and $b$ can be divided into groups of $d$, then $a$ can be constructed by combining these groups, implying that $a$ is also divisible by $d$.

def gcd(a, b):
    assert a >= 0 and b >= 0 and a + b > 0

    while a > 0 and b > 0:
        if a >= b:
            a = a - b
        else:
            b = b - a

    return max(a, b)

print(gcd(24, 16))
print(gcd(790933790547, 1849639579327))
# The following call would take too long
# print(gcd(790933790548, 2))

This implementation directly follows the definition of the GCD by repeatedly subtracting the smaller number from the larger one until one of them becomes zero.

However, for large numbers, this approach can be inefficient due to the potentially large number of subtractions. In this example, $gcd(981564621485124,84)$ we see lots of subtractions.

Why the Modulo Operator $a$ % $b$ is More Efficient

A more efficient approach involves using the modulo operator (%) to find the remainder when one number is divided by another.

This is because the modulo operation directly gives us the "leftover" part after division, eliminating the need for repeated subtractions.

Consider the following revised implementation:

def gcd_efficient(a, b):
    while b != 0:
        a, b = b, a % b
    return a

This recursive version is more concise and efficient than the iterative one. Here's a breakdown of why the modulo operator is more efficient:

• Direct Calculation:   The modulo operator calculates the remainder in a single operation, avoiding the need for multiple subtractions.

• Reduced Iterations:   By directly jumping to the remainder, the algorithm reduces the number of iterations required to find the GCD, especially for large numbers.

• Quicker Convergence:   The modulo operation ensures that the numbers involved in the calculation become smaller more rapidly, leading to faster convergence to the GCD.

To illustrate the difference in efficiency, consider the following example:

Calculating the GCD of $790933790548$ and $2$ using repeated subtraction would involve subtracting $2$ from the larger number billions of times. However, using the modulo operator, the algorithm would quickly determine that the remainder is $0$, and hence the GCD is $2$.

While both the repeated subtraction and modulo-based approaches are correct, the modulo-based implementation is significantly more efficient, especially for larger numbers.

By directly calculating the remainder, the modulo operator reduces the number of iterations required and leads to a faster convergence to the GCD. Therefore, the modulo-based approach is the preferred method for implementing Euclid's algorithm in practice.

The Iterative Process

Euclid's algorithm employs a repetitive process to determine the GCD:

• Initialization:   Start with two non-negative integers, $a$ and $b$.

• Remainder Calculation:   If a is greater than $b$, replace a with the remainder of $a$ divided by $b$. Otherwise, replace $b$ with the remainder of $b$ divided by $a$.

• Termination:   Repeat step $2$ until one of the numbers becomes zero. The non-zero number at this point is the GCD of the original $a$ and $b$.

A Step-by-Step Example

Let's illustrate Euclid's algorithm with a concrete example:

Example:  Find the GCD of $120$ and $84$.

Initial values: $a=120$, $b=84$

1. Iteration:  $120$ % $84=36$.  New values: $a=84$, $b=36$

2. Iteration:  $84$ % $36=12$.  New values: $a=36$, $b=12$

3. Iteration:  $36$ % $12=0$.  The algorithm terminates.

The GCD of $120$ and $84$ is $12$.

The Recursive Approach

While the iterative approach is intuitive, Euclid's algorithm can also be implemented recursively:

def gcd_recursive(a, b):
    if b == 0:
        return a
    else:
        return gcd_recursive(b, a % b)

The number of iterations required by Euclid's algorithm is bounded by the logarithm of the larger input number. This makes it extremely efficient, even for very large numbers.

In practice, the algorithm typically converges much faster than this theoretical upper bound.

Applications

Euclid's algorithm has numerous applications, including:

• Diophantine Equations:   Solving equations involving integers.

• Continued Fractions:   Generating continued fraction representations of real numbers.

• Modular Arithmetic:   Computing modular inverses and solving linear congruences.

• Cryptography:   Underlying various cryptographic algorithms, such as RSA.

Conclusion

Euclid's algorithm is a fundamental algorithm in number theory, providing an efficient and elegant solution for calculating the greatest common divisor of two integers.

Its applications extend to various fields, making it an essential tool in mathematics and computer science.

Extended Euclid's Algorithm

Introduction

  The Extended Euclidean Algorithm is a fundamental algorithm in number theory that not only computes the greatest common divisor (GCD) of two integers but also provides coefficients that express the GCD as a linear combination of these integers. $$gcd(a,b)=a\cdot x+b\cdot y$$

This additional information is invaluable in various mathematical and cryptographic applications.

The Standard Euclidean Algorithm

  Before delving into the extended version, let's briefly review the standard Euclidean Algorithm. It's a method for finding the GCD of two non-negative integers.

The algorithm repeatedly applies the division algorithm to obtain a sequence of remainders until a remainder of $0$ is reached. The last non-zero remainder is the GCD.

Example:   $gcd(888,54)$

Let's apply the Euclidean algorithm to find the GCD of $888$ and $54$:

• Step 1:  $888=54\cdot (16)+24$

• Step 2:  $54=24\cdot (2)+6$

• Step 3:  $24=2\cdot (12)+0$

Since the remainder is $0$, the GCD is the last non-zero remainder, which is $6$.

$$gcd(888,54)=6$$

In summary, the Euclidean algorithm is a simple yet efficient method for finding the GCD of two numbers.

It involves repeated division and remainder calculations until a remainder of $0$ is reached. The last non-zero remainder is the GCD.

Extending the Algorithm

  The Extended Euclidean Algorithm builds upon the standard algorithm by introducing two auxiliary sequences of integers. These sequences, often denoted as $x$ and $y$, are calculated at each step of the algorithm and are used to express the current remainder as a linear combination of the original two numbers.

Formal Description:

Given two non-negative integers $a$ and $b$, the Extended Euclidean Algorithm calculates integers $g$, $x$, and $y$ such that:

$$g=gcd(a,b)$$ $$g=ax+by$$

Our main goal is to see which $x$ and $y$ value multiplication produces the number pair whose gcd we know. We are actually putting Euclid's operations in reverse order.

Example:   $gcd(888,54)=888x+54y$

Given:

$a=888$   $b=54$   $gcd(888,54)=6$   (as calculated using the standard Euclidean algorithm)

Goal:

Find integers $x$ and $y$ such that   $6=888x+54y$

Steps:

• Step 1:  $6=54-24\cdot 2$  So,  $6=54+24\cdot (-2)$

• Step 2:  $6=54+(888-54\cdot (16))\cdot (-2)$

• Step 3:  $6=54+888\cdot (-2)+54\cdot (-32)$  So,  $6=54\cdot (-33)+888\cdot (-2)$

Rearranging to match the desired form: $$6=888\cdot (-2)+54\cdot 33$$

Final Solution:

Therefore, for the equation $6=888x+54y$, the values of $x$ and $y$ are:

$$x=-2$$ $$y=33$$

So, $gcd(888,54)$ can be expressed as:

$$6=888\cdot (-2)+54\cdot 33$$

The Algorithm

def extended_gcd(a, b):
  assert a >= b and b >= 0 and a + b > 0

  if b == 0:
    d, x, y = a, 1, 0
  else:
    (d, p, q) = extended_gcd(b, a % b)
    x = q
    y = p - q * (a // b)

  assert a % d == 0 and b % d == 0
  assert d == a * x + b * y
  return (d, x, y)

Explanation

• Function Definition:

  extended_gcd(a, b):  This defines a function that takes two non-negative integers, $a$ and $b$, as input and returns a tuple containing the greatest common divisor (GCD) d, and the coefficients $x$ and $y$ such that $d=ax+by$.

• Preconditions:

  assert a >= b and b >= 0 and a + b > 0:  Ensures that the input numbers are valid for the algorithm. a must be greater than or equal to b, both must be non-negative, and their sum must be greater than $0$.

• Base Case:

  if b == 0: d, x, y = a, 1, 0:  If b is 0, the GCD is $a$, and the coefficients are $1$ and $0$, respectively. This is the base case of the recursion.

• Recursive Case:

  (d, p, q) = extended_gcd(b, a % b):  Recursively calls the function with b and the remainder of $a$ divided by $b$. This is the core of the Euclidean algorithm.

  x = q:  The coefficient $x$ is assigned the value of $q$ from the recursive call.

  y = p - q * (a // b):  The coefficient $y$ is calculated using the values of $p$, $q$, and the integer division of $a$ by $b$. This step is crucial for expressing the GCD as a linear combination of $a$ and $b$.

• Postconditions:

  assert a % d == 0 and b % d == 0:  Verifies that the calculated GCD $d$ divides both $a$ and $b$.

  assert d == a _ x + b _ y:  Ensures that the calculated GCD $d$ can be expressed as a linear combination of $a$ and $b$ using the coefficients $x$ and $y$.

• Return Value:

  return (d, x, y):  Returns a tuple containing the GCD $d$ and the coefficients $x$ and $y$.

Applications

The Extended Euclidean Algorithm has numerous applications, including:

• Modular Arithmetic:

  • Finding modular inverses:  Given two relatively prime integers $a$ and $n$, the algorithm can be used to find an integer $x$ such that $a\cdot x\equiv 1(modn)$ . This is crucial in cryptography for operations like decryption.

  • Solving linear Diophantine equations:  Equations of the form $a\cdot x+b\cdot y=c$ can be solved efficiently using the algorithm.

• Cryptography:

  • RSA algorithm:  The Extended Euclidean Algorithm is used to compute the private key in the RSA cryptosystem.

  • Diffie-Hellman key exchange:  It is used to compute the shared secret key.

• Number theory:

  • Continued fractions:  The algorithm can be used to find the continued fraction representation of a rational number.

Conclusion

  The Extended Euclidean Algorithm is a fundamental algorithm with far-reaching implications in number theory and cryptography.

Its ability to compute the GCD and provide coefficients for a linear combination makes it an essential tool for solving various mathematical problems.

By understanding the principles behind this algorithm, one can gain a deeper appreciation for its applications in modern cryptography and computer science.

Applications

Least Common Multiple

  The least common multiple ($lcm$) is a fundamental concept in number theory, with applications ranging from simple arithmetic to advanced algorithms.

In essence, the $lcm$ of two integers is the smallest positive integer that is divisible by both numbers.

This concept is crucial in various mathematical operations, especially when dealing with fractions and rational numbers.

Definition and Properties

  Formally, the least common multiple of two non-zero integers, $a$ and $b$, denoted as $lcm(a,b)$, is the smallest positive integer that is divisible by both $a$ and $b$. It is undefined if either $a$ or $b$ is zero.

Key properties of the $lcm$ include:

• Commutativity:  $lcm(a,b)=lcm(b,a)$

• Associativity:  $lcm(a,lcm(b,c))=lcm(lcm(a,b),c)$

• Distributivity:  $lcm(a,bc)=lcm(lcm(a,b),c)$

• Relationship with Greatest Common Divisor ($gcd$):  $lcm(a,b)\cdot gcd(a,b)=|ab|$

Applications of the $lcm$

The $lcm$ finds numerous applications in various mathematical and computational contexts:

• Fractions:  When adding or subtracting fractions, the lcm of the denominators is used to find a common denominator.

• Modular Arithmetic:  The $lcm$ is used to determine the least common period of periodic functions in modular arithmetic.

• Scheduling Problems:  In scheduling problems, the $lcm$ is used to find the earliest time at which two or more events can occur simultaneously.

• Number Theory:  The $lcm$ is a fundamental concept in number theory, used in various theorems and algorithms.

Algorithms for Computing the $lcm$

Several algorithms can be used to compute the $lcm$ of two integers:

Brute Force Method

The simplest approach is to iterate through all integers from $1$ to the product of $a$ and $b$, checking if each integer is divisible by both $a$ and $b$. The first such integer is the $lcm$.

def lcm_naive(a, b):

  max_num = max(a, b)

  while True:
    if max_num % a == 0 and max_num % b == 0:
      return max_num
    max_num += 1

Using the $gcd$

 A more efficient method is to use the relationship between the $lcm$ and the $gcd$:

The $lcm$ and $gcd$ of two numbers are closely related. The equation $$lcm(a,b)\cdot gcd(a,b)=a\cdot b$$ states that the product of the $lcm$ and $gcd$ of two numbers is equal to the product of the two numbers.

When we multiply the $gcd$ and $lcm$, we are essentially "canceling out" the common factors and ending up with the product of the original numbers.

def gcd(a, b):
    #Calculates the GCD of two numbers using the Euclidean algorithm.

    while b != 0:
        a, b = b, a % b

return a

def lcm_efficient(a, b):
    #Calculates the LCM of two numbers using the GCD.

return (a * b) // gcd(a, b)

Why is this more efficient?

• Naive approach:  Simple to understand but can be very slow for large numbers, especially if the $lcm$ is much larger than the inputs.

• Euclidean algorithm approach:  More complex but significantly faster, especially for larger numbers. It leverages a well-established algorithm for calculating the $gcd$ and a direct formula to compute the $lcm$.

In conclusion, while the naive approach is straightforward, the Euclidean algorithm-based approach is generally preferred for its efficiency and elegance. The relationship between $lcm$ and $gcd$ provides a powerful tool for calculating the $lcm$ in a computationally efficient manner.

Conclusion

  The least common multiple is a fundamental concept in number theory with widespread applications. Understanding its properties and algorithms for computing it is essential for various mathematical operations and problem-solving tasks.

Diophantine Theorem

  Diophantine equations, named after the ancient Greek mathematician Diophantus of Alexandria, are polynomial equations with integer coefficients that seek integer solutions.

A Simple Example: The Candy Problem

  You have a $$5$ bill and want to buy $$2$ candies. The cashier only has $$3$ coins. How many $$5$ bills should you give, and how many $$3$ coins will you receive in return?

We can represent this situation with the equation: $$5x=2y+5$$

where $x$ is the number of $$5$ bills and $y$ is the number of $$3$ coins.

A solution to this equation is $x=3$ and $y=5$, meaning you give the cashier $3$ $$5$ bills and receive $5$ $$3$ coins in change.

The Case of $187x+55y=121$

  This equation is more complex, but it still follows the same principle of seeking integer solutions. One solution is $x=3$ and $y=-8$.

However, what's intriguing is that this equation has infinitely many solutions. This means there are countless pairs of $x$ and $y$ that satisfy the equation.

The Puzzle of Solvability

  Not all Diophantine equations have solutions. The equation $187x+55y=45$, for instance, has no integer solutions. This begs the question: What factors determine whether a Diophantine equation has a solution?

Now we will explorer how we can solve this theorem with the help of the Euclid algorithm.

Solving Diophantine Equations with Euclid's Algorithm

The simplest form of a Diophantine equation is the linear equation: $$ax+by=c$$

where $a$, $b$, and $c$ are integers. A fundamental theorem states that this equation has a solution if and only if the greatest common divisor of $a$ and $b$ divides $c$.

The extended Euclidean algorithm is a powerful tool for finding solutions to linear Diophantine equations. This algorithm not only computes the greatest common divisor of two integers but also finds coefficients that express the greatest common divisor as a linear combination of the two integers.

Let's we see this in example:

Example:   $10x+6y=14$

Do not forget! The main porpuse ise finding $x$ and $y$.

1. Find the gcd:  $$gcd(10,6)=2$$

2. Use the extended Euclidean algorithm:  $$gcd(10,6)=2=10\cdot (-1)+6\cdot 2$$

3. Multiply by c:  To get $10x+6y=14$, we multiply both sides of the previous equation by 7, obtaining $$14=10\cdot (-1)\cdot 7+6\cdot 2\cdot 7$$ $$14=10\cdot (-7)+6\cdot 14$$ So, one solution is $$x=-7,y=14$$

4. Find all solutions:  All solutions can be expressed as $$x=-7+10t$$$$y=14-6t$$ where $t$ is any integer.

Consider the equation $$4x+6y=9$$

Here, the greatest common divisor $gcd$ of $4$ and $6$ is $2$.

However, $2$ does not divide $9$ evenly. Therefore, this equation has no integer solutions.

To determine if a Diophantine equation has a solution, we find the greatest common divisor of the coefficients of the variables. If this greatest common divisor does not divide the constant term evenly, then the equation has no integer solutions.

Modular Division

Modular division is a mathematical operation that involves finding the remainder when a number is divided by another number called the modulus.

Multiple Inverse

In modular arithmetic, a modular inverse of a number a modulo $m$ is $a$ number $b$ such that:

$$a\cdot b\equiv 1(modm)$$

This means that when you multiply $a$ and $b$ and then divide by $m$, the remainder is $1$. Think of it like finding a number that "undoes" the multiplication by a within a specific modular system.

Let's find the modular inverse of $3$ modulo $7$. Possible modular inverses $1,2,3,4,5,6$

$$3\cdot 1\equiv 3(\mathrm{mod}7)$$ $$3\cdot 2\equiv 6(\mathrm{mod}7)$$ $$3\cdot 3\equiv 2(\mathrm{mod}7)$$ $$3\cdot 4\equiv 5(\mathrm{mod}7)$$ $$3\cdot 5\equiv 1(\mathrm{mod}7)$$

So, the modular inverse of $3$ modulo $7$ is $5$.

Key points to remember:

• Not every number has a modular inverse for every modulus.
• The Euclidean algorithm is a common method for finding modular inverses.
• Modular inverses are essential for solving linear congruences and other problems in modular arithmetic.

Uniqueness of Inverses

In modular arithmetic, not all numbers have a unique inverse. This means that two different numbers can have the same inverse when working with a specific modulus.

Example:

Let's consider the modulus $7$.

The inverse of $2$ modulo $7$ is $4$ because $2\cdot 4\equiv 1(\mathrm{mod}7)$

The inverse of $5$ modulo $7$ is also $4$ because $5\cdot 4\equiv 1(\mathrm{mod}7)$

As you can see, both $2$ and $5$ have the same inverse ($4$) modulo $7$.

This phenomenon occurs due to the cyclical nature of modular arithmetic, where numbers wrap around within a fixed range.

Existence of Inverses

In modular arithmetic, not all numbers have a modular inverse. The existence of an inverse depends on the relationship between the number and the modulus.

A number a has a modular inverse modulo $m$ if and only if $a$ and $m$ are coprime. This means that their greatest common divisor $gcd$ is $1$.

Why is coprimality important?

When $a$ and $m$ are coprime, there exists a linear combination of $a$ and $m$ that equals $1$. This linear combination can be used to find the modular inverse of $a$.

Example:

Let's consider the modulus $10$.

• The number $3$ is coprime with $10$ because their $gcd$ is $1$.

  Therefore, $3$ has a modular inverse modulo $10$.

• The number $5$ is not coprime with $10$ because their $gcd$ is $5$.

  Therefore, $5$ does not have a modular inverse modulo $10$.

Extended Euclidean Algorithm

  The Extended Euclidean Algorithm is a powerful tool for calculating modular inverses. It not only finds the greatest common divisor $gcd$ of two numbers but also expresses the $gcd$ as a linear combination of them. This linear combination is crucial for determining the modular inverse.

Delving Deeper with Examples

I want to describe this just numbers and equations.

What is the $x$?   $17x\equiv 1(\mathrm{mod}43)$

First we must write $17$ and $43$ in the form of the extended Euclidean algorithm as $ax+by=c$

$$43=17\cdot 2+9$$

$$17=9\cdot 1+8$$

$$9=8\cdot 1+1$$

We have reached the remainder $1$, now let's substitute it in reverse and write it.

First we leave $1$ alone

$$1=9-8\cdot 1$$

$$1=9-(17-(9\cdot 1))\cdot 1$$

$$1=9-(17-9)$$

$$1=17\cdot (-1)+9\cdot 2$$

$$1=17\cdot (-1)+(43-(17\cdot 2))\cdot 2$$

$$1=17\cdot (-1)+43\cdot 2+17\cdot (-4)$$

$$1=17\cdot (-5)+43\cdot 2$$

If we take $(\mathrm{mod}43)$ of both sides of the equation

$$1(\mathrm{mod}43)=17\cdot (-5)$$

Wait, what is that? Isn't this equation the same as our question? We clearly see that $x$ is $-5$.

In fact, we are using the extended Euclidean algorithm in all the steps in this example and the answer we have at the end is.

Integer Factorization

  Number theory is not only an old and beautiful branch of mathematics, but is also (surprise!) practically useful in an everyday sense. When you pay with a credit card or connect to a website, cryptographic protocols using number-theoretic tools operate behind the scenes.

In this chapter, we discuss some of these tools.

The most popular number-theoretic cryptographic protocol, RSA (invented by Rivest, Shamir and Adleman and published around 1977) is based on our ability to generate large prime numbers and on our inability to factor large integers in a reasonable time.

We will discuss this algorithm in detail later. Currently, it is under attack because quantum computers may be able to factor large integers at some point in the future.

That said, the danger is (for now) mostly theoretical, and the RSA protocol continues to be widely used. It is an exciting time to be learning number theory, when advanced cryptographic attacks need to be deterred and many potential replacement protocols (thought to be more secure against quantum attacks) are rooted in number-theoretic concepts.

Prime Numbers

You can easily arrange $12$ balls in three rows and four columns

This worked because $4\cdot 3=12$. In other words, because $12$ can be represented as a product of two smaller numbers, $3$ and $4$.

The question to ask is: "How many groups of $12$ apples are possible?" $$(2,6)(6,2)(3,4)(4,3)$$

Note that we do not include trivial decompositions like $12=1\times 12=12\times 1$ (a rectangle with one row or one column).

On the other hand, $23$ does not have any non-trivial decompositions (only $1\times 23$ and $23\times 1$), meaning it is prime.

Definition

  A prime number is a positive integer $p>1$ that cannot be represented as the product of two smaller positive integers.

A number $p>1$ is prime if it does not have positive integer divisors except for $1$ and $p$.

Indeed, if $m=uv$ is composite where $u$ and $v$ are non-trivial divisors, then $u$ and $v$ are both smaller than $m$, making it impossible for either one to be equal to $1$. And if a number $m>1$ has some non-trivial divisor $d$, then for some positive integer $q$ we must have $m=dq$ by the definition of a divisor, and neither $d$ nor $q$ can be equal to $1$, so both must be smaller than $m$.

Naive Approach - Trial Divison

  The most straightforward method to determine if a number is prime is through trial division. We divide the number by all integers from $2$ up to its square root. If none of these divisions result in a remainder of $0$, the number is prime.

def is_prime_naive(num):
  """Checks if a number is prime using trial division."""
  if num <= 1:
    return False
  for i in range(2, int(num**0.5) + 1):
    if num % i == 0:
      return False
  return True

The provided Python function, is_prime_naive, efficiently determines whether a given integer is a prime number. It first handles the base case where the number is less than or equal to $1$, which is not prime. The function then iterates through potential divisors from $2$ up to the square root of the number.

If any divisor divides the number evenly, it's not prime and the function returns False. If the loop completes without finding a divisor, the number must be prime, and the function returns True. This optimization of checking only up to the square root is based on the mathematical property that if a number has a divisor greater than its square root, it must also have a corresponding divisor less than its square root.

Factoring

  Every integer $m>1$ can be represented as the product of primes: there exists a positive integer $k$ and primes $p_1,\dots ,p_k$ such that $m=p_1\dots p_k$.

Existence

What happens if $m$ is prime?

In this case, $k=1$ and $p_1=m$. So the phrase "product of primes" should not be taken too literally: in this case there is only one (prime) number in the "product" and the product is equal to this number. (One could even allow $m=1$ by considering an "empty product" with no factors that is equal to $1$, but we will not go that far.)

Note also that we do not require the $p_1,\dots ,p_k$ to all be distinct: for example, $$4=2\cdot 212=3\cdot 2\cdot 2$$

Prove the Theorem

  Let us look at this statement from the algorithmic point of view: given some $m>1$, how can we find a prime decomposition (existence of which we want to prove)?

If $m$ is prime, we already know that this decomposition consists of $m$ only. What if $m$ is composite (not prime)?

By definition then, $m=uv$ for some $u,v$ where $1<u,v<m$. How can we then find the decomposition of $m$?

It is easy:  just combine the decompositions of $u$ and $v$, forming a long product from the two shorter ones. Both $u$ and $v$ are smaller that $m$, so we may assume (by induction in our proof, or a recursive call in our algorithm) that for $u$ and $v$ the decompositions exist and can be found.

# Finds the minimal divisor>1 of the given integer m>1
def min_divisor(m):
    for d in range(2, m + 1):
        if m % d == 0:
            return d
        # optimization:
        if d * d > m:
            return m


def is_prime(m):
    return m == min_divisor(m)


def factoring(m):
    if is_prime(m):
        return [m]
    else:
        divisor = min_divisor(m)
        factors = factoring(m // divisor)
        factors.append(divisor)
        return factors

  The numbers of the form $2^{2^n}+1$ were considered long ago by Pierre Fermat (1607--1665, Wikipedia), famous for the Last Fermat theorem; we will see the other result of him later in this chapter. He noticed that $2^0,2^1+1,2^2+1,2^4+1,2^8+1,2^{16}+1$ are all primes and conjectured that all subsequent numbers are also prime.

Only later Leonhard Euler (1707--1783,Wikipedia) discovered the factorization of $2^{32}+1$ in 1732, and more than a century after that was needed to find the factorization of $2^{64}+1$. Now our simple program gives these factorization in seconds. (But do not forget two optimization lines, otherwise it would take much longer.)

For the next Fermat numbers one should use more advanced factorization algorithms. There is a module sympy in python that provides function factorint that factors $2^{128}+1$ and $2^{256}+1$ in minutes, but Fermat numbers grow really fast (and only few more factorizations are known, even if we use the most advanced factorization tools).

Unique Factoring

Decomposition of an integer $m>1$ into a product of prime factors is essentially unique. The word essentially here means that we ignore the ordering of the factors: they can be permuted in any way and we still get the same decomposition. For example, $$12=2\cdot 2\cdot 3=2\cdot 3\cdot 2=3\cdot 2\cdot 2$$

First, let us note that we can group identical factors in the decomposition. In this we get a product of the form $$m=p_1^{n_1}{p}_2^{n_2}...p_k^{n_k}$$

Here all $p_i$ are different, and all $n_i$ are positive integers (the number of occurrences of $p_i$ in the factorization).

The number $n_i$ is called the multiplicity of a prime $p_i$ in $m$. If $p_i$ does not appear in the decomposition, we say that the multiplicity of $p_i$ in $m$ equals zero. (This sounds natural since we may add fictional term $p_i^0=1$ in the factoring.)

Divisors and Multiplicity

Complete the statement: an integer $d>1$ is a divisor of an integer $m>1$ if and only if the multiplicity of $p⟨\dots ⟩$ for every prime $p$.

The last part can be filled as follows: if the multiplicity of $p$ in $d$ does not exceed the multiplicity of $p$ in $m$, for every prime $p$. Indeed, imagine that $d$ is a divisor of $m$, i.e., that $m=dq$ for some $q$. Then the (unique) factorization of $m$ is obtained by concatenating the factorizations of $d$ and $q$. Therefore, the multiplicity of every prime $p$ in $m$ is the sum of its multiplicities in $d$ and $q$, and is greater or equal than the multiplicity of $p$ in $d$.

On the other hand, if every prime appears in the factorization of $m$ at least as many times as for $d$, then we can add missing factors to $d$ to obtain $m$. If $q$ is the product of these missing factors, then $dq=m$, so $d$ divides $m$.

Problem

Consider all the positive divisors of $2^4{3}^3=432$. How many of them do exist (including trivial divisiors $1$ and $432$)?

As the previous problem shows, all the divisors have the form $2^k{3}^l$ where $0\le k\le 4$ and $0\le l\le 3$. For $k=l=0$ we get $1$, for $k=4$ and $l=3$ we get $432$. We may list all of them systematically: $$2^0\cdot 3^0=1$$ $$2^0\cdot 3^1=3$$ $$2^0\cdot 3^2=9$$ $$2^0\cdot 3^3=27$$ $$2^0\cdot 3^4=81$$ $$2^1\cdot 3^0=2$$ $$2^1\cdot 3^1=6,...$$

We do not need to write them all explicitly; we have only to count them. Each of five powers of $2$ (i.e., $2^0,2^1,2^2,2^3,2^4$) is combined with four powers of $3$ (i.e., $3^0,3^1,3^2,3^3$), so we get $5\times 4=20$ combinations that lead (as we know) to $20$ divisors.

Chinese Remainder Theorem

When dividing numbers $0,1,2,3,\dots$ by (say) $5$, we get remainders

$0,1,2,3,4,0,1,2,3,4,0,1,2,\dots :$ this repeats all the time. In general, $m$ and $m+5$ have the same remainder ($m\equiv m+5(mod5)$, their difference is divisible by $5$).

What if we consider the remainders for two different modulo at the same time?

First of all, we choose a pair like $2$ and $3$ for dividing a number for example $15$.

• The remainders modulo $2$ (i.e., $0$ and $1$) alternate (even values of $i$ alternate with odd values of $i$).

• The remainders modulo $3$ (i.e., $0,1,2$) appear in a $3$-loop ($0,1,2,0,1,2,\dots$)

• When we come to six, both cycles return to their original position (since $6$ is divisible both by $2$ and $3$, and then the pairs start to repeat, thus forming a loop of length $6$).

• All six possible combinations of remainders (two possible remainders modulo $2$ combined with three possible remainders modulo $3$) appear in this sequence (once per a $6$-loop).

Let us look at the column for $2$ and $4$: we see a cycle of length $4$ in this column formed by pairs $(0,0),(1,1),(0,2),(1,3)$ - and, indeed, $4$ is divisible both by $2$ and $4$, so we get again the pair $(0,0)$. Note that not all combinations of remainders appear in the cycle: for example, pair $(1,2)$ does not appear.

Can you explain why this pair does not appear: why there are no m such that $m\equiv 0(mod4)$ and $m\equiv 1(mod6)$?

Again, the reason is simple: numbers of the form $4u+0$ are even, while numbers of the form $6v+1$ are odd.

To understand the behavior of remainders, it is useful to look at bigger examples, and draw the pairs of remainders on a coordinate plane. This can be done with the following code (do not worry if you do not understand the options, they are needed to make nice plots).

import matplotlib.pyplot as plt

a, b = 10, 5
n = a * b

plt.plot([i % a for i in range(n)], [i % b for i in range(n)],
         color='green', linestyle='dashed', linewidth=3,
         marker='o', markerfacecolor='blue', markersize=12)

plt.axis('square')
plt.xlim(-1, a)
plt.ylim(-1, b)
plt.xlabel(f'm mod {a}')
plt.ylabel(f'm mod {b}')

plt.savefig('crt-10-5.png')

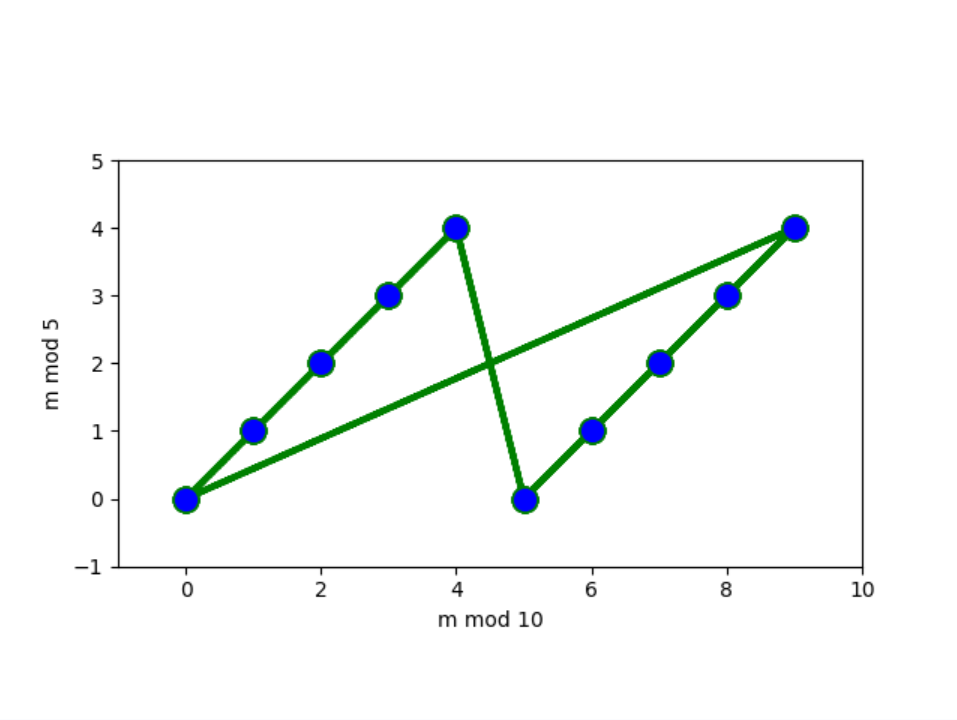
In the first picture, the remainder modulo $10$ determines the remainder modulo $5$. Indeed, if $m=10k+r$, then $10k$ is divisible by $5$, so $mmod5=rmod5$.

A similar picture for $mmod13$ and $mmod7$ looks different:

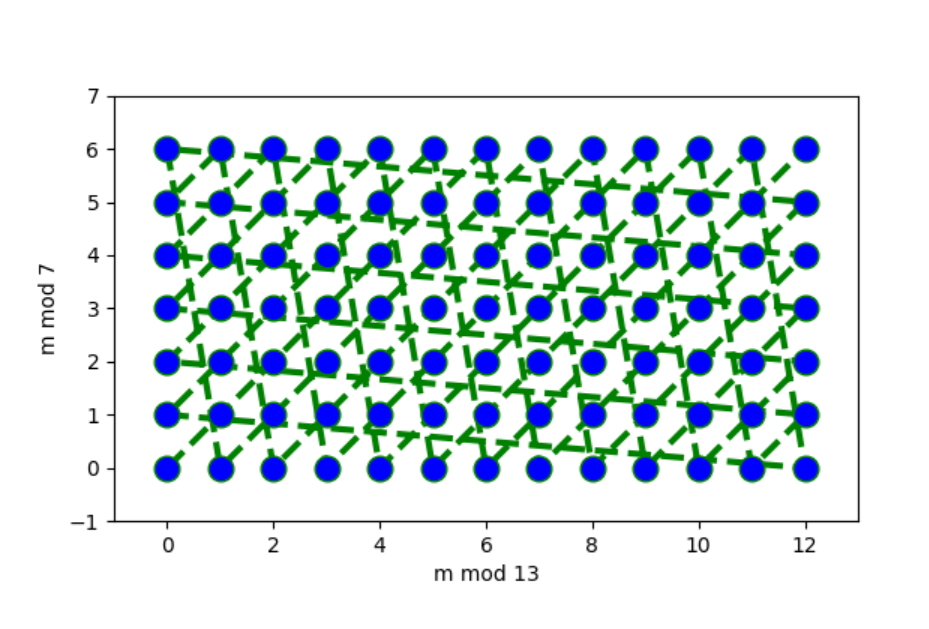
Here we see that all pairs of remainders are possible. Why? This question is answered by the Chinese remainder theorem.

Theorem

Let $p,q$ be coprime. Then the system of equations $$x=a(modp)$$ $$x=b(modq)$$

has a unique solution for $x$ modulo $pq$.

The reverse direction is trivial: given $x\in {\mathbb{Z}}_{{}_{pq}}$ we can reduce $x$ modulo $p$ and $x$ modulo $q$ to obtain two equations of the above form.

The following is a general construction to find a solution to a system of congruences using the Chinese remainder theorem:

1. Compute $N=n_1\times n_2\times \cdots \times n_k$

2. For each $i=1,2,\dots ,k$ compute $$y{}_i=\frac{N}{n{}_i}=n_1\cdot n_2+\cdots +n_{{}_{i-1}}\cdot n_{{}_{i+1}}+\cdots +n{}_k$$

3. For each $i=1,2,\dots ,k$ compute $z_i\equiv y_i^{-1}mod{n}_i$ using Euclid's extended algorithm ($z_i$ exists since $n_1,n_2,\dots ,n_k$ are pairwise coprime).

4. The integer $x={{\sum }^k}_{{}_{i=1}}{a}_i{y}_i{z}_i$ is a solution to the system of congruences, and $xmodN$ is the unique solution modulo $N$.

When a system contains a relatively small number of congruences, an efficient process exists to apply the Chinese remainder theorem.

Solve the system of congruences

$$x\equiv 1mod3$$ $$x\equiv 4mod5$$ $$x\equiv 6mod7$$ Take all the yi and construct the integer: $$M=a_1{M}_1{y}_1+a_2{M}_2{y}_2+...+a_r{M}_r{y}_r$$ We can prepare our situation to this: $$a_1=1a_2=4a_3=6$$ $$M_1=5\cdot 7M_2=3\cdot 7M_3=3\cdot 5$$ We wrote $x_n^{-1}$ instead $y_n$ for inverse $$x=5\cdot 7\cdot 1\cdot x_1^{-1}+3\cdot 7\cdot 4\cdot x_2^{-1}+3\cdot 5\cdot 6\cdot x_3^{-1}$$ $$\text{for mod 3}\text{ for mod 5}\text{ for mod 7}$$ For find to general $x$ solve inverses of $x$ values $$M_n\cdot x_n^{-1}=1\mathrm{mod}(m)$$ For $x_1^{-1}$: $$5\cdot 7\cdot x_1^{-1}\equiv 1\mathrm{mod}(3)$$ $$3\cdot x_1^{-1}\equiv 1\mathrm{mod}(3)$$ We can use extended euclid algortihm $$3=2\cdot 1+1$$ $$1=3-2\cdot 1$$ $$x_1^{-1}=-1=2$$ find all $x$ values like this: $$x_2^{-1}=1,x_3^{-1}=1$$ and combine together: $$x=(5\cdot 7\cdot 1\cdot 2+3\cdot 7\cdot 4\cdot 1+3\cdot 5\cdot 6\cdot 1)\mathrm{mod}(3\cdot 5\cdot 7)$$ $$x=(70+84+90)\mathrm{mod}(105)$$ $$x=(244)\mathrm{mod}(105)$$ $$x=(34)\mathrm{mod}(105)$$

Question-1 :  A box contains gold coins.

If the coins are equally divided among six friends, four coins are left over.

If the coins are equally divided among five friends, three coins are left over.

If the box holds the smallest number of coins that meets these two conditions, how many coins are left when equally divided among seven friends?

See answer ▼

Answer : 0

First of all, mathematize the question. $$x\equiv 4\mathrm{mod}(6),x\equiv 3\mathrm{mod}(5)$$ So, $$x\equiv y\mathrm{mod}(7)?$$ We can prepare our situation $$a_1=4,a_2=3$$ $$M_1=5,M_2=6$$ $$x=5\cdot 4\cdot x_1^{-1}+6\cdot 3\cdot x_2^{-1}$$ $$\text{for mod 6}\text{for mod 5}$$ For $x_1^{-1}$ and $x_2^{-1}$ : $$5\cdot x_1^{-1}\equiv 1\mathrm{mod}(6)$$ $$6\cdot x_2^{-1}\equiv 1\mathrm{mod}(5)$$ $$x_1^{-1}=5,x_2^{-1}=1$$ general equation: $$x=(5\cdot 5\cdot 4+6\cdot 3\cdot 1)\mathrm{mod}(6\cdot 5)$$ $$x=118\mathrm{mod}(30)$$ $$x=28\mathrm{mod}(30)$$ we found $28$ gold in our box. Now divide among seven friends $$28\equiv y\mathrm{mod}(7)$$ $$0\equiv y\mathrm{mod}(7)$$ Opps, zero coins left after divided our friends :)

Example

Find $x$, if possible, such that $$2x\equiv 5\mathrm{mod}(7)$$ $$3x\equiv 4\mathrm{mod}(8)$$

Solution First note that $2$ has an inverse modulo $7$, namely $4$. So we can write the first equivalence as $x\equiv 4\cdot 5\equiv 6\mathrm{mod}(7)$. Hence, we can multiply every side of equation with inverse of $2$. $$2\cdot 4\cdot x\equiv 5\cdot 4\mathrm{mod}(7)$$ $$8\cdot x\equiv 20\mathrm{mod}(7)$$ and we reached simple equation $$x\equiv 6\mathrm{mod}(7)$$ do it same process for other $$3\cdot 3\cdot x\equiv 4\cdot 3\mathrm{mod}(8)$$ $$x\equiv 4\mathrm{mod}(8)$$ We can revise the question again and solve it like the previous ones. I left this to you :)

Fast Modular Exponentiation

  Our next results (Fermat's little theorem and its generalization, Euler's totient theorem) deal with modular exponentiation, i.e., with expressions of type $a^b\mathrm{mod}(c)$ where $a,b,c$ are integers. But before stating and proving this result, let us discuss the purely algorithmic question: how to compute $a^b\mathrm{mod}(c)$ reasonably fast?

How would you compute $314^{271}\mathrm{mod}(123)$ and $314159265358^{2718281828}\mathrm{mod}(123456789)$ ?

Computing this in python directly gives the following result:

print((314 ** 271) % 123)
print((314159265358 ** 2718281828) % 123456789)

# 38
# it will be crashed...

If you try this code on your computer, you can see that your computer is struggling. Because we know that pc uses which methot. This method consists of taking the exponent of the number and then taking its modulo.

The right way to compute modular exponentiation in python is to use the built-in pow method. The following code produces the result in the blink of an eye. We will learn what is going on under the hood below.

print((314 ** 271) % 123)
print((314159265358 ** 2718281828) % 123456789)

# 38
# 32073907

Problem

Compute $8^{100}\mathrm{mod}(63)$.

Of course, starting with computing $8^{100}$ is a bad idea. Note that $8^2=64\equiv 1\mathrm{mod}63$, and $$8^{100}=8^2\cdot 8^2\cdot 8^2\text{ ... }{8}^2\equiv 1\cdot 1\cdot 1\cdot 1\text{ ... }1\mathrm{mod}(63)$$ hence the answer is $1$.

Problem

Prove that $2^{1001}+3^{1001}$ is divisible by $5$.

We know $3\equiv (-2)\mathrm{mod}(5)$. If we write $-2$ instead of $3$. $$2^{1001}+(-2{)}^{1001}$$ And it is equal to zero. So, it's divisible by $5$.

Problem

Find $2^{1025}\mathrm{mod}(17)$.

Since $2^{1024}=16^{256}\equiv (-1{)}^{256}\equiv 1\mathrm{mod}(17)$, answer is $2$.

  Now we can compute $a\mathrm{mod}c$, $a^2\mathrm{mod}c$, $a^3\mathrm{mod}c$, ... sequentially, multiplying each time by $a$ and keeping only the remainder modulo $c$. In this way we do not need to store large numbers (only numbers smaller than $c$). Does this approach work for our example $314159265358^{2718281828}\mathrm{mod}(123456789)$?

The size of numbers is no more a problem, but we need to perform $2718281827$ multiplications --- too many. Can we do better? This is a general question for computing powers (that makes sense not only for modular computations).

Let $x$ be some number. Can you compute $x^{64}$ in less than 63 multiplications (that would be needed if we compute $x$, $x^2$, $x^3$, ..., $x^{64}$ sequentially)?

For this problem the answer is especially easy to guess, since $64=2^6$ and repeated squaring helps: $$x^2=x\cdot x,x^4=x^2\cdot x^2,x^8=x^4\cdot x^4,x^{16}=x^8\cdot x^8,x^{32}=x^{16}\cdot x^{16},x^{64}=x^{32}\cdot x^{32}.$$

In this way the exponents grow faster ($\times 2$ instead of $+1$ at every step), and we use only $6$ multiplications.

In general, to compute $x^n$ for $n=2^k$ we need $k={\log }_{2}n$ multiplications.

For $x^{65}$ we may multiply $x^{64}$ by $x$. Since we have also computed previous powers of 2, we may use that $x^{68}=x^{64}\cdot x^4$ and $x^{77}=x^{64}\cdot x^8\cdot x^4\cdot x$ (note that $77=64+8+4+1$). Similar trick can be used in the general.

def fast_modular_exponentiation(b, e, m):
    assert m > 0 and e >= 0
    if e == 0:
        return 1
    if e == 1:
        return b
    if e % 2 == 0:
        return fast_modular_exponentiation((b * b) % m, e // 2, m)
    else:
        return (fast_modular_exponentiation(b, e - 1, m) * b) % m


print(fast_modular_exponentiation(123456789222, 456788, 598723))

# 32073907

The program implementing this idea computes $314159265358^{2718281828}\mathrm{mod}123456789$ in a fraction of a second.

Problem

Prove that the number of multiplications when computing $x^n$ (for $n\ge 1$) both in this program and in the method described above (using binary notation) is the same: $$(\text{number of bits in }n)+(\text{number of ones in }n)-2$$ where counting the bits and ones in $n$ we use the binary representation of $n$.

It turns out that this is not exactly the minimal number of multiplications needed to compute $x^n$. For example, for $x^{15}$ we get 6 multiplications with both our approaches, while one can compute it in 5 multiplications:

$x^2=x\cdot x;x^4=x^2\cdot x^2;x^5=x^4\cdot x;x^{10}=x^5\cdot x^5;x^{15}=x^{10}\cdot x^5.$

See Wikipedia article about addition chains that minimize the number of multiplications.

Fermat's Little Theorem

Introduction

  Fermat's Little Theorem, a fundamental result in number theory, provides a powerful tool for understanding the behavior of integers modulo a prime number. It has far-reaching implications in various fields, including cryptography, computer science, and pure mathematics.

The Theorem

Fermat's Little Theorem states that if $p$ is a prime number and $a$ is an integer not divisible by $p$, then: $$a^{p-1}\equiv 1\mathrm{mod}p$$

In other words, if we raise $a$ to the power of $p-1$ and divide the result by $p$, the remainder will always be $1$.

Proof

  To prove Fermat's Little Theorem, we will consider the set of integers $1,2,3,...,p-1$. We will multiply each element of this set by $a$ modulo $p$:

$$a,2a,3a,...,(p-1)a$$

No two of these numbers are congruent modulo $p$. To see why, suppose that $ia\equiv ja(modp)$ for some $1\le i,j\le p-1$. Then, $p$ would divide $(i-j)a$. Since $p$ does not divide $a$, it must divide $i-j$. However, $\mid i-j\mid <p$, so this is impossible.

Therefore, the set $a,2a,3a,...,(p-1)a$ is a rearrangement of the set $1,2,3,...,p-1$ modulo $p$. Multiplying all the elements of these sets together, we get:

$$a\cdot 2a\cdot 3a\cdot ...\cdot (p-1)a\equiv 1\cdot 2\cdot 3\cdot ...\cdot (p-1)(modp)$$

Simplifying, we obtain:

$$a^{p-1}(p-1)!\equiv (p-1)!\mathrm{mod}p$$

Since $(p-1)!$ is not divisible by $p$, we can cancel it from both sides, leaving us with:

$$a^{p-1}\equiv 1\mathrm{mod}p$$

This completes the proof of Fermat's Little Theorem.

Problems and Solutions

Problem 1:

Find the remainder when $2^{100}$ is divided by $11$.

Solution:

Since $11$ is a prime number, we can apply Fermat's Little Theorem:

$2^{10}\equiv 1(mod11)$

Therefore, $$2^{100}=(2^{10}{)}^{10}\equiv 1^{10}\equiv 1(\mathrm{mod}11)$$

So, the remainder when $2^{100}$ is divided by $11$ is $1$.

Problem 2:

Find the last digit of $3^{1001}$.

Solution:

The last digit of a number is equivalent to its remainder when divided by $10$. So, we need to find $3^{1001}\mathrm{mod}10$.

We can not use Fermat's Theorem in this problem. Because $p$ is not prime. Think another way:

Note that $3^4\equiv 1(\mathrm{mod}1)0$. Therefore, $$3^{1001}=3^{4\cdot 250+1}\equiv (3^4{)}^{250}3\equiv 1^{250}3\equiv 3(\mathrm{mod}10)$$

Hence, the last digit of $3^{1001}$ is $3$.

Conclusion

  Fermat's Little Theorem is a powerful tool with wide-ranging applications in number theory and computer science. Its elegant proof and practical utility make it a cornerstone of modern mathematics.

As we continue to explore the depths of number theory, Fermat's Little Theorem will undoubtedly remain a valuable asset in our mathematical toolkit.

Euler's Totient Theorem

  At its core lies Euler’s Totient Function, denoted $\varphi (n)$, which counts the integers up to $n$ that are coprime with $n$. This seemingly simple concept has profound implications, ranging from pure mathematics to cryptography.

Key Concepts in Euler's Totient Theorem

1. Definition of $\varphi (n)$:

The totient function $\varphi (n)$ is defined as:

$$\varphi (n)=\text{Number of integers }k\text{ such that }1\le k\le n\text{ and }\text{gcd}(k,n)=1.$$

Example:

For $n=12$:

$$\begin{gathered} 1,\cancel{2},\cancel{3},\cancel{4},5,\cancel{6},7,\cancel{8},\cancel{9},\cancel{10},11. \\ \text{Coprime integers: }[1,5,7,11] \end{gathered}$$

Thus, $\varphi (12)=4$.

What happens with prime numbers?

Prime numbers has only one prime factor: itself!

Example

For $n=5$:

$$\begin{gathered} 1,2,3,4,\cancel{5}. \\ \text{Coprime integers: }[1,2,3,4] \end{gathered}$$

Thus, $\varphi (5)=4$.

This is generally true of all prime numbers:

$$\begin{gathered} \varphi (p)=p-1 \\ \text{where p is a prime number} \end{gathered}$$

We have our first timesaver.

2. Multiplicative Property:

If $m$ and $n$ are coprime ($\text{gcd}(m,n)=1$), then:

$$\varphi (mn)=\varphi (m)\cdot \varphi (n).$$

Example:

For $m=5,n=6$:

$$\begin{gathered} \varphi (5)=4, \\ \varphi (6)=2, \\ \varphi (30)=\varphi (5)\cdot \varphi (6)=4\cdot 2=8. \end{gathered}$$

3. Prime Factorization Formula:

For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_k^{{\alpha }_k}$:

$$\varphi (n)=n\cdot \prod _{i=1}^k\left(1-\frac{1}{p_i}\right)$$

Example:

For $n=60=2^2\cdot 3\cdot 5$:

$$\varphi (60)=60\cdot \left(1-\frac{1}{2}\right)\cdot \left(1-\frac{1}{3}\right)\cdot \left(1-\frac{1}{5}\right),$$

$$\varphi (60)=60\cdot \frac{1}{2}\cdot \frac{2}{3}\cdot \frac{4}{5}=16.$$

Applications of Euler's Totient Theorem

1. Primality Testing:

For a prime $p$:

$$\varphi (p)=p-1.$$

This property aids in testing whether a number is prime.

2. RSA Encryption:

RSA relies on the totient function to generate keys:

• Let $n=p\cdot q$, where $p,q$ are primes. $$\varphi (n)=(p-1)(q-1).$$

Example: For $p=11,q=13$:

$$\begin{gathered} n=143, \\ \varphi (143)=10\cdot 12=120. \end{gathered}$$

Public and private keys are derived using $\varphi (n)$, ensuring secure encryption.

3. Applications in Modular Arithmetic and Prime Numbers:

a) Efficient Exponentiation:

Using the property $a^{\varphi (n)}\equiv 1(\mathrm{mod}n)$ for $a$ coprime to $n$, large powers modulo $n$ can be computed efficiently.

Example: Calculate $7^{100}(\mathrm{mod}12)$:

1. Since $\varphi (12)=4$, $7^4\equiv 1(\mathrm{mod}12)$.
2. Break $100$ into $4\cdot 25$: $7^{100}=(7^4{)}^{25}\equiv 1^{25}\equiv 1(\mathrm{mod}12)$.

b) Properties of Primes in Modular Arithmetic:

Prime numbers simplify modular inverses, as every nonzero element in ${\mathbb{Z}}_p$ is coprime to $p$.

Example: Modular Inverses:

Find the modular inverse of $3(\mathrm{mod}7)$:

1. $\varphi (7)=6$, so $3^6\equiv 1(\mathrm{mod}7)$.
2. Use powers to find $3\cdot x\equiv 1(\mathrm{mod}7)$: $$3\cdot 5\equiv 15\equiv 1(\mathrm{mod}7).$$ Thus, $5$ is the modular inverse of $3$ under mod $7$.

  Euler's Totient Theorem stands as a testament to the interplay between theory and application, bridging the gap between abstract mathematics and real-world cryptography. Its elegance and utility continue to inspire mathematicians and engineers alike.

History of Cryptography

  Cryptography made its greatest advancements during World War I and II, driven by the need for secure communication amidst rampant espionage. Early ciphers proved insufficient, and secure communication required frequently changing shared keys—an increasingly complex task as global communication expanded. This challenge led to the creation of the RSA cryptosystem, enabling secret key exchange without fear of eavesdropping. We will also explore common vulnerabilities in RSA implementations and conduct a few targeted attacks.

After the war, cryptographic methods became crucial for global power, particularly in nuclear defense systems and computer networks. Early radar systems transmitted alerts through these networks, allowing swift decision-making. Universities soon adopted computer networks, paving the way for innovations like online commerce, messaging systems, and digital currencies. Today, secure communication methods form the backbone of technologies we rely on daily.

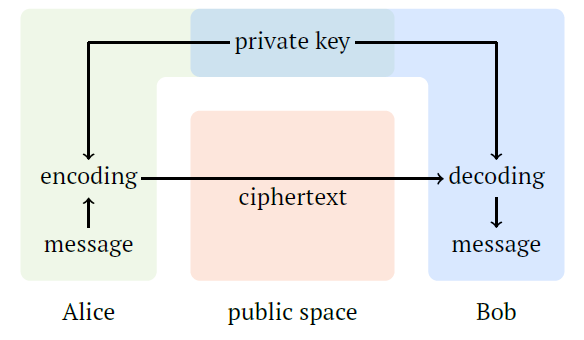
Alice and Bob, the traditional placeholders in cryptography, represent any two parties exchanging information securely. Eve, the eavesdropper, listens to everything sent between them.

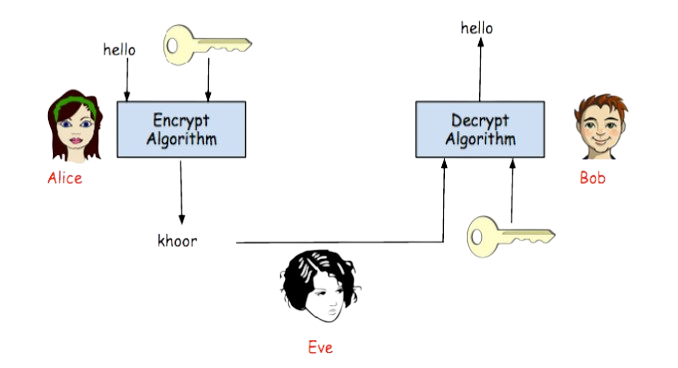
To ensure privacy, Alice encrypts her plaintext message into ciphertext, which only Bob can decrypt. Various cipher systems enable this, balancing efficiency with security to outpace potential attackers like Eve.

Caesar Encryption

  If the key is a cyclic shift of the alphabet is known as Caesar cipher. It is named after Julius Caesar, who used it for establishing secure communication. A key for such an encryption scheme can be generated using a physical device like the one shown below:

Key: Shift the alphabet by N letters to create cipher alphabet

In example on below, every letter is replaced by a letter three places further in the alphabet. Nowadays, it is not recommended to use Caesar cipher as it is too easy to crack it.

Encryption

Decryption

The reason why this cipher is easily breakable is that the space of possible keys is small. Indeed, there are only $26$ different cyclic shifts of the alphabet: the possible values of the shift are $0,1,\dots ,25$. This makes it possible for Eve to enumerate all the keys and to decode using each of them.

ciphertext = 'kyv wzmv sfozex nzqriuj aldg hlztbcp'
for shift in range(26):
    key = alphabet[shift:] + alphabet[:shift]
    print(decode(ciphertext))

# try and find plain text

Substitution Ciphers

  Substitution cipher is one of the oldest and simplest. To use it, Alice and Bob share a private key that represents a permutation of the letters, e.g.,

jsuyfhkpicomxrqatlbvznewgd

To encode her message, Alice starts by aligning the key with the alphabet:

abcdefghijklmnopqrstuvwxyz

jsuyfhkpicomxrqatlbvznewgd

Then, she uses the resulting substitution table as follows: she replaces every letter $a$ in her message by $j$, every $b$ by $s$, and so on. For decoding, one uses the same substitution table with the two rows switched: $j$ is replaced by $a$, $s$ is replaced by $b$, and so on. It is particularly easy to implement this cipher in python:

alphabet = 'abcdefghijklmnopqrstuvwxyz'
key =      'jsuyfhkpicomxrqatlbvznewgd'


def substitute(text, substitute_what, substitute_by):
    result = ''
    for symbol in text.lower():
        if symbol in substitute_what:
            result += substitute_by[substitute_what.index(symbol)]
        else:
            result += symbol

    return result


def encode(plaintext):
    return substitute(plaintext, alphabet, key)


def decode(ciphertext):
    return substitute(ciphertext, key, alphabet)


message = 'the quick brown fox jumps over the lazy dog'
code = encode(message)
print(code)
print(decode(code))

"The quick brown fox jumps over the lazy dog" is a well-known pangram, that is, a sentence containing all letters of the alphabet. For this reason, it is widely used for testing fonts.

When the key is not just a cyclic shift of the alphabet, but rather an arbitrary permutation of the alphabet, enumerating all keys is not that easy: the size of the space of all keys is $$26!=403291461126605635584000000$$

Cracking Simple Substitution

 Substitution ciphers are not considered secure as they are vulnerable to frequency analysis attacks. Such attacks exploit the fact that some letter combinations appear more frequently in English texts than others: the letters $e,t,a,o$ are the most common; the word $the$ usually appears many times.

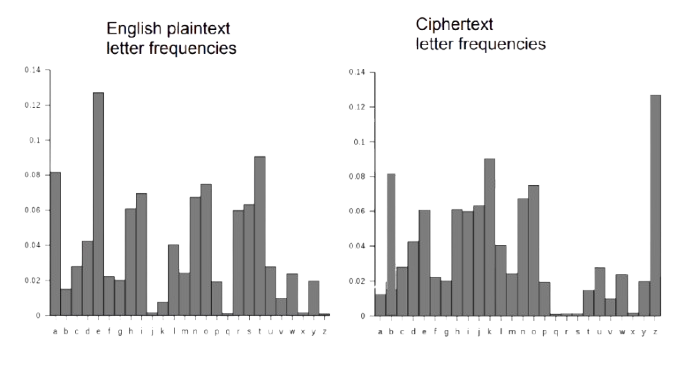
Did something catch your attention? $26!$ We don't need to try twice. We can solve the problem simply by assuming that the letter z in the encrypted text is equal to the letter e.

One-Time Pad

This section focuses on an encryption scheme that is both invulnerable to frequency analysis and provably secure. In fact, it guarantees that an eavesdropper, Eve, gains no information from the intercepted ciphertext.

Imagine Alice needs to send a single bit of information to Bob, such as buy or sell, attack or retreat. They can agree in advance on a pair of text messages (e.g., cat and dog) to represent these options, along with their meanings. If Eve intercepts the message but doesn’t know the agreed code, the information remains completely inaccessible to her.

To explain in terms of bit operations, assume Alice’s message is a single bit $m$ ($0$ or $1$), and the private key $k$, known only to Alice and Bob, is also a single bit. The ciphertext $c$, transmitted over a public channel, is calculated as $c=m\oplus k$, where $\oplus$ represents $XOR$ (exclusive OR). For example, if $k=0$, the ciphertext equals the message ($c=m$). If $k=1$, the ciphertext is the reverse of the message ($c=m\oplus 1$). To decode, Bob simply computes $m=c\oplus k$.

Extending to Multi-Bit Messages

The one-time pad can be generalized to longer messages. To encode a bit string, each bit is XORed with a corresponding bit from the private key. For example, if Bob sends the bit string $1000110100$ and the key is $1111111111$, the ciphertext becomes $0111001011$, where each plaintext bit is XORed with the respective key bit. Decoding reverses the operation: $m_i=c_i\oplus k_i$.

Limitations of a Single-Bit Key

While the one-time pad is theoretically secure, it requires keys as long as the messages themselves. Using a single-bit key repeatedly, as demonstrated, is insecure. Eve could try both possible keys ($0$ and $1$) to decode the ciphertext. For example, if Bob encrypts a PIN code, Eve could easily guess it by testing both keys.

The Perfect Security of One-Time Pads

To achieve true security, Alice and Bob must use a unique, secret key for each bit of the message. For a message $m_1,m_2,\dots ,m_n$ , they agree on a private key $k_1,k_2,\dots ,k_n$ and compute $c_i=m_i\oplus k_i$ for each bit. This approach ensures that Eve gains no information from the ciphertext. Regardless of the intercepted data, all $2^n$ possible original messages appear equally likely to Eve.

This scheme, known as a symmetric private-key method, is illustrated below: encoding and decoding are symmetric, and the private key is shared between Alice and Bob. Patented in 1919, the one-time pad remains a cornerstone of cryptographic history, though its practical use is often limited by the need for key management.

Many Time Pad Attack

  The many-time pad attack exploits a critical vulnerability of reusing a one-time pad (OTP) key across multiple messages. While the OTP is perfectly secure when a unique key is used for each message, reusing the same key compromises security. Let’s understand why.

Suppose Alice and Bob use the same key $k$ for two distinct plaintext messages $m_1$ and $m_2$. The ciphertexts generated are $c_1=m_1\oplus k$ and $c_2=m_2\oplus k$. An eavesdropper, Eve, intercepting both ciphertexts, can compute their XOR:

$$c_1\oplus c_2=(m_1\oplus k)\oplus (m_2\oplus k)=m_1\oplus m_2$$